Zamknij się i rachuj czyli tajemnice mechaniki obrotu BS na konkretnym przykładzie. 1

    Interpretacje to każdy może sobie pisać do woli ale dopiero rachunki pokazują poprawność i skuteczność interpretacji i  bezlitośnie obnażają każdą najmniejszą niedoskonałość. Jak się okazało mimo że sporo już potrafię to nadal są elementy z którymi mam problemy. Myślałem że uda mi się już przedstawić rachunek w całości ale utknąłem i muszę spisać co udało mi się już policzyć aby zamknąć ten etap i pójść dalej.

    Ten sam schemat w dwóch różnych układach odniesienia

Mamy więc wektory

    Ponieważ mamy przypadek że wektory prędkości są do siebie równoległe i przeciwnie skierowane to wyznaczając linie między tymi punktami oraz linie zaczepioną o wektory prędkości tych punktów to ich przecięcie wyznaczą punkt na chwilowej osi obrotu na której znajduje się też wektor prędkości kątowej. Jeżeli wyznaczymy prostą zaczepioną o wektory pędu to przecięcie tej prostej z prostą między punktami wyznaczy punkt osi na której znajduje się wektor momentu pędu.

    Tu jest taka dziwna sytuacja (co będzie widać za chwilę), że punkty według wektorów przyspieszeń obracają się wokół chwilowej osi obrotu na której jest wektor prędkości kątowej, a biorąc pod uwagę wektory sił wskażą oś na której znajduje się wektor momentu pędu.

    Wektory przyspieszeń punktów wyznaczy nam wzór na siłę dośrodkową

 i schemat ich rozłożenia

    Wektory przyspieszeń zawsze się zerują ale różnica w masach m₁=1 i m₂=2 powoduje że zmieniają się nieproporcjonalnie wektory pędów i wektory sił. Konsekwencją tego jest powstanie niezerowych różnych momentów sił F_1y , F_2x.

    Musimy pamiętać że te dwa punkty nie są pełnym obrazem Bryły Sztywnej i muszą istnieć jeszcze co najmniej dwa punkty. Aby uprościć są one symetryczne i też wyniki będą symetryczne dlatego do tej pory je pomijałem

    Jak widać na schemacie wyliczone wektory sił można rozłożyć na składowe centralne, skierowane do środka ciężkości które zawsze się zerują, oraz składowe sił prostopadłe wektora położenia których skutkiem jest powstawanie momentów sił.

    Jak policzyć momenty sił z tych wektorów siły?  Wystarczy zastosować wzór na moment siły a własności równania iloczynu wektorowego samo skoryguje wektor siły ignorując składową równoległą (centralną)

    Sprawdzenie z mojego wzoru

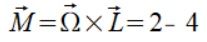
    Liczyłem to już wielokrotnie na wiele różnych sposobów i zawsze weryfikacja jest pozytywna.

    Wektor przyspieszenia kątowego zazwyczaj nie jest równoległy do wektora momentu siły https://youtu.be/8OnWhW1-15s ,

dlatego musimy wyliczyć odwrotność tensora momentu bezwładności

    Jest to przypadek szczególny gdzie wektor momentu siły jest równoległy do wektora przyspieszenia kątowego, tym łatwiej będzie wykonać następny krok.

    Dużo tego było ale po przez spisanie tego zamknąłem ten etap i mogę przejść do następnego.

Reakcja

0%0Pozytywnie0%0Neutralnie 0%0Negatywnie

Twoje emocje

0%0Lubię to!

0%0Super0%0Ekscytujący 0%0Ciekawy0%0Smieszny0%0Smutny0%0Wściekły0%0Przerażony0%0Szokujący0%0Wzruszający0%0Rozczarowany0%0Zaskoczony

Co sądzisz?

0%0Prawda0%0Manipulacja0%0Fake news

0

0Ulub

Oryginalne źródło ZOBACZ