“Prędkość kątowa – wielkość wektorowa opisująca ruch obrotowy (np. ruch po okręgu) ciała. Jest wektorem (pseudowektorem) leżącym na osi obrotu ciała i skierowanym zgodnie z regułą śruby prawoskrętnej.”
https://pl.wikipedia.org/wiki/Pr%C4%99dko%C5%9B%C4%87_k%C4%85towa
Ale czym jest obiekt zdefiniowany jako “ciało”? Co jeżeli chcemy obrócić obiekt wirtualny, taki jak chociażby wektor lub punkt czy układ odniesienia? Czy możemy do tego użyć pseudowektora prędkości kątowej? Z definicji w większości podręczników nie za bardzo wiadomo czy takie obiekty również można stosować do tego wektora.
Pisałem o tym parokrotnie ale napisze jeszcze raz. Wszelkiego typu wektory czy wzory matematyczne są jedynie ludzkimi interpretacjami rzeczywistości, bardzo często dobrze odwzorowujące rzeczywistość ale same w sobie rzeczywiste nie są, są jedynie naszym ludzkim sposobem rozumienia rzeczywistości. Nikt nigdy nie zobaczy żadnego rzeczywistego wektora czy wzoru pod mikroskopem, czy za pomocą jakiegokolwiek innego urządzenia, ponieważ jest to twór czysto wirtualny, nieistniejący w przyrodzie.
Prędkość kątowa nie jest wektorem który rzeczywiście posiada jakiekolwiek ciało, jak ziemia czy księżyc, a jest jedynie wirtualnym matematycznym tworem w którym są zapisane informacje na temat poruszania się punktu, a dopiero punkt ten może imitować jakieś ciało fizyczne, jak ziemia czy księżyc. Pseudo wektor prędkości kątowej jest abstrakcją wyższego rzędu przechowującą informacje o abstrakcyjnych wektorach, prędkości punktu i jego przyspieszenia dośrodkowego (a ściślej doosiowego).
Prędkość kątowa nie jest innym rodzajem (odmiennym) ruchu względem prędkości prostoliniowej a jest to szczególny przypadek prędkości prostoliniowej, gdy zmiana prędkości w czasie jest prostopadła do prędkości prostoliniowe. Niniejszy schemat jest dużym uproszczeniem gdyż punkt posiada prędkość liniową ale ze względu na działające przyspieszenie nie porusza się po linii prostej.
Moja definicja:
Pseudowektor prędkości kątowej jest to wielkość wektorowa opisująca ruch dowolnego punktu (również wektora) w przestrzeni, który jest szczególnym przypadkiem prędkości liniowej (przemieszczenia się punktu) na którą działa przyspieszenie (zmiana prędkości) prostopadłe do tej prędkości. Jest pseudowektorem leżącym na osi obrotu ciała i skierowanym zgodnie z regułą śruby prawoskrętnej.
Aby było jasne, pod względem geometrii wektorów ich dodawanie, odejmowanie, mnożenie czy obracanie odbywa się w ten sam sposób i dla operacji matematycznych nieistotne jest co dany wektor sobą reprezentuje. Dlatego też obracanie każdego wektora odbywa się tak samo i to co zauważyłem w moich badaniach można go opisać za pomocą wektora obrotu.
Wyniku działania wektora obrotu O na wektor A powstaje zmiana wektora dA która jest wynikiem iloczynu wektorowego tych dwóch wektorów.
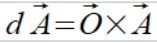
Pseudowektor obrotu ma zastosowanie do każdego wektora, prędkość kątowa jest szczególnym przypadkiem wektora obrotu odnosząca się do prędkości punktu. Obrót wektora charakteryzuje się zmianą kierunku wektora wzdłuż tej zmiany ale nie zmienia wartości bezwzględnej tego wektora.
Można teraz dokonać obrotu wektora prędkości (przyspieszenie dośrodkowe), obrotu krętu (nieefektywny moment siły) czy też obrócić wektor prędkości kątowej
Dlaczego o tym pisze? Dawno temu chciałem wiedzieć jak działa przyspieszenie kątowe prostopadłe do prędkości kątowej, czy też jak dział moment siły prostopadły wektora krętu. Pytałem wielu i nikt nie wiedział. Być może ktoś już kiedyś to opisywał ale być może ta wiedza została zapomniana albo nikt nie szukał odpowiedzi na te pytania. Dla mnie to co tu opisałem powinno być w każdym podręczniku a nie było w żadnym materiale do którego ja dotarłem. Problem polega na tym że Fizycy uznali temat za zamknięty i nikt nie jest zainteresowany wszczęciem dyskusji na temat uzupełnienia wiedzy czy poprawienie niewielkich błędów.
Zgłoś naruszenie/Błąd
Pozytywnie
Neutralnie 
Negatywnie
Lubię to!
Super
Ekscytujący 
Ciekawy
Smieszny
Smutny
Wściekły
Przerażony
Szokujący
Wzruszający
Rozczarowany
Zaskoczony
Prawda
Manipulacja
Fake news
Oryginalne źródło ZOBACZ
Dodaj kanał RSS
Musisz być zalogowanym aby zaproponować nowy kanal RSS